Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Unschärferelation II
Auf dieser Seite erwarten Sie polarisierende Wirkungen, die aus Wellen Teilchen machen …
www.wissenstexte.de > Physik-Wissen > Optik > Beugung > Welle-Teilchen-Dualismus
Beugung und der Welle-Teilchen-Dualismus
Bei der Besprechung der Strahlenoptik haben wir das Licht einfach als Strahlen angesehen; um die Beugungsphänomene zu erläutern, mussten wir Licht als Welle betrachten. Es gibt aber auch Effekte, die man nur erklären kann, wenn man Licht als Teilchen auffasst, wie beispielsweise der Fotoeffekt.
Fotoeffekt
Beim Fotoeffekt werden Elektronen durch Licht aus einem Festkörper herausgeschlagen. Um das zu schaffen, muss zum einen die Energie, mit der die Elektronen im Atomverband festgehalten werden, überwunden werden, zum andern müssen die Elektronen beschleunigt werden. Bei Lichtwellen würde man davon ausgehen, dass Licht höherer Intensität die Elektronen stärker beschleunigt – je mehr Licht, desto schnellere Elektronen. Das ist aber nicht so. Statt dessen muss das Licht eine bestimmte Mindestenergie haben. Ist die Energie des Lichtes zu klein, nützt auch eine Erhöhung der Intensität nichts – es werden keine Elektronen freigesetzt. Hat das Licht aber diese Mindestenergie, kann es Elektronen aus dem Festkörper schlagen.
Das ist nur zu deuten, indem man sich Licht als Teilchen vorstellt. Bereits ein einziges Lichtteilchen, das die nötige Mindestenergie hat, reicht aus, um ein Elektron aus dem Festkörper zu schlagen. Nimmt man mehrere Photonen, erhöht man also die Intensität des Lichtes, erhöht sich die Anzahl der herausgeschlagenen Elektronen, aber nicht deren Geschwindigkeit. Um die Geschwindigkeit zu erhöhen, braucht man Lichtteilchen mit höherer Energie.
Welle-Teilchen-Dualismus
Tatsächlich hat Licht die Eigenschaften beider – Welleneigenschaften und Teilcheneigenschaften, denn Photonen sind quantenmechanische Objekte, also völlig andersartige Objekte. Man nennt diese Eigenschaft, sowohl Wellen- als auch Teilcheneigenschaften zu haben, Welle-Teilchen-Dualismus. Je nachdem, welche seiner Eigenschaften man misst, zeigt ein Quantenobjekt sich mehr als Teilchen oder mehr als Welle. Die Beschreibungen bestimmter Phänomene im Wellen- oder im Teilchenbild sind immer nur Vereinfachungen, um es unserer Anschauung leichter zu machten.
Im Prinzip betrifft dies alle Objekte – nur sind bei makroskopischen Objekten die Wellenlängen so klein, dass man deren Welleneigenschaften vernachlässigen und beispielsweise einen Schrank oder einen Kieselstein als reines Teilchen betrachten kann. Elementarteilchen wie bspw. Elektronen sind jedoch Quantenobjekte, die ebenfalls Welleneigenschaften haben.
Unschärferelation
Die von Werner Heisenberg gefundene Unschärferelation oder Unbestimmtheitsrelation besagt, dass bestimmte Paare von Eigenschaften eines Teilchens, wie beispielsweise Ort und Impuls, nicht gleichzeitig beliebig genau gemessen werden können. Je genauer man das eine misst, desto ungenauer wird die Messung des anderen. Wird der Ort exakt gemessen, also ohne jede Messungenauigkeit, kann man über den Impuls überhaupt keine Aussage mehr treffen. Umgekehrt gilt dasselbe. Das ist keine Folge von unausgereifter Messtechnik oder der Schusseligkeit des wissenschaftlichen Personals, sondern eine prinzipielle Eigenschaft der Natur. (Allerdings sind Messungen ohne jede Messungenauigkeit nicht möglich, sodass zu der quantenmechanischen Unbestimmtheit immer noch Messungenauigkeiten dazu kommen.)
Diese Unbestimmtheit hängt mit dem Welle-Teilchen-Dualismus zusammen – je genauer die Position eines Photons bekannt ist, desto ungenauer kennt man seinen Impuls. Der Impuls eines Photons ist aber proportional zu seiner Wellenlänge. Je genauer also der Ort eines Photons bekannt ist, desto weniger genau kennt man seine Wellenlänge und umgekehrt. Ein monochromatischer Wellenzug – also einer mit einer einzigen exakten Wellenlänge – ist unendlich lang. Sein Ort ist also vollkommen unbestimmt. Da seine Wellenlänge eindeutig ist, ist sein Impuls dagegen exakt bestimmt.
Eine Welle mit begrenzter räumlicher Ausdehnung – also ein Gebilde, dessen Amplitude überall außerhalb dieser Ausdehnung null ist – erhält man nur, wenn man Wellen mehrerer Wellenlängen überlagert. Denn nur eine solche Überlagerung vieler Wellenlängen führt zu einer Auslöschung der Wellen außerhalb der Ausdehnung. Ein solches Wellenpaket hat also einen sehr genau bekannten Ort, aber einen unbekannten Impuls, da es ja aus vielen Wellenlängen zusammengesetzt ist und jede dieser Wellenlängen einem anderen Impuls entspricht.
Nun wird man eine unendlich ausgedehnte Welle am ehesten als Welle bezeichnen, ein eng begrenztes Wellenpaket dagegen am ehesten als Teilchen auffassen können. Mit anderen Worten: Betrachtet man ein Photon als räumlich eingegrenztes Wellenpaket oder Teilchen, sind seine Welleneigenschaften nicht mehr feststellbar. Umgekehrt gilt das Gleiche: Der monochromatische, unendlich ausgedehnte Wellenzug hat keine Teilcheneigenschaften.
Beides – Teilchen- und Wellenbild – sind jedoch nur idealisierte Grenzfälle mit begrenzter Gültigkeit. Je nach Beobachtung ist das eine oder andere mehr oder weniger gültig. (Das Gesagte gilt nicht nur für Photonen – auch Teilchen wie Elektronen haben Welleneigenschaften und unterliegen dem Welle-Teilchen-Dualismus.)
Welcher-Weg-Information: Der Welle-Teilchen-Dualismus im Experiment sichtbar gemacht
Bestimmt man den Ort eines Photons (mehr oder weniger) genau, zeigt es sich einem also als Teilchen; misst man seinen Impuls oder lässt den Ort unbestimmt, sieht man seine Welleneigenschaften.
Das kann man mit relativ einfachen Mitteln auch im Heimlabor feststellen. Dieses Experiment habe ich in Heft 7/2007 von Spektrum der Wissenschaft gefunden („Der Quantenradierer“ von Rachel Hillmer und Paul Kwiat, S. 68) und natürlich selbst ausprobiert – die Beschreibung meiner eigenen Versuche finden Sie im übernächsten Abschnitt. Man braucht Polarisationsfolie, Klebefilm, Pappe, Draht, einen Laser-Pointer, Alufolie und ein Gummiband. Polarisationsfolie bekommt man unter anderem bei www.astromedia.de.
Bitte beachten: Niemals direkt in einen Laser hineinsehen! Es besteht die Gefahr ernsthafter Augenschäden!
Polarisation
Lichtwellen sind elektromagnetische Wellen, sie bestehen also aus schwingenden elektrischen und magnetischen Feldern. Schwingen nun die elektrischen Felder aller im Lichtstrahl enthaltenen Wellenzüge in derselben Ebene, nennt man das Licht polarisiert. (Da die magnetischen Felder senkrecht zu den elektrischen gerichtet sind, schwingen diese dann auch alle in einer Ebene. Es ist aber üblich, die Richtung der elektrischen Felder für die Angabe der Polarisation zu nutzen.) Licht kann beispielsweise vertikal polarisiert sein (wenn die elektrischen Felder alle „von oben nach unten“ schwingen) oder horizontal polarisiert (wenn die elektrischen Felder alle „von rechts nach links“ schwingen), aber natürlich auch in jedem beliebigen Winkel dazwischen. Näheres zur Polarisation finden Sie unter Polarisation.
Ein Polfilter (hergestellt aus Polarisationsfolie) lässt nur Licht einer Polarisationsrichtung durch. Ist das Licht beispielsweise horizontal polarisiert, die Polfolie aber vertikal ausgerichtet, kommt kein Licht hindurch. Vertikal polarisiertes Licht dagegen käme ungehindert durch. Licht, das in einem anderen Winkel zur Richtung der Polfolie polarisiert ist, kommt zu einem bestimmten Anteil durch – beträgt der Winkel bspw. 45°, sind es 50 Prozent.
Das Experiment
Dieses Experiment lässt sich ohne Weiteres zu Hause durchführen. Es zeigt, wie man Interferenzmuster verschwinden lassen kann, indem man die Ortsunbestimmtheit beseitigt.
Der Laser-Pointer wird mit Alufolie umwickelt. In die Folie wird vorn mit einer Nadel ein Loch als Blende gestochen. Mithilfe des Gummibandes wird der Schalter arretiert, damit der Laser-Pointer dauerhaft angeschaltet bleibt. Nun wird zunächst der Draht vor den Laserstrahl gesetzt. Abbildung 1 zeigt den Versuchsaufbau. In etwa 2 m Entfernung stellt man einen Schirm auf (Pappe oder so etwas). Trifft der Laserstrahl auf den Draht, wird er in zwei Teile zerlegt, von denen der eine rechts, der andere links am Draht vorbeigeht. Die links und rechts am Draht vorbeilaufenden Teilwellen werden am Draht gebeugt und überlagern sich dann wieder. Auf dem Schirm kann man nun ein Interferenzmuster beobachten, das durch die Interferenz des Lichtes, das rechts am Draht vorbeigeht mit jenem, das links vorbeigeht, entsteht (Abbildung 2).
Die Interferenzmuster, die hinter einem Draht entstehen, entsprechen dann denen eines Doppelspalts, wenn gewährleistet ist, dass der Spaltabstand groß ist gegen die Spaltbreite (siehe Intensitäten). Diese Beugungsbilder wurden aber nun nicht mit einem Spalt, sondern mit einem Laser-Pointer und einem Draht gewonnen. (Der Draht ist 0,3 mm dick; es handelt sich um schwarz lackierten Basteldraht.) Der Abstand der beiden Spalten des Doppelspaltes entspricht im Experiment hier also der Dicke des Drahtes. Die einzelnen Spalte sind so breit wie das, was vom Lichtstrahl rechts und links am Draht vorbeiläuft. Durch die Verengung des Laserstrahls mit der Alufolienblende geht nur sehr wenig vom Lichtstrahl rechts und links am Draht vorbei – was gleichbedeutend ist mit einer im Vergleich zum Spaltabstand (= Drahtdicke) kleinen Spaltbreite. (Siehe auch unten am Ende der Seite.)
- Abb. 1 ¦ Versuchsaufbau I

- Man sieht, dass es auch mit krummen Drähten funktioniert …
- Abb. 2 ¦ Beugungsbild hinter einem Draht

- Die Schiefe der Linien kommt daher, dass ich das Foto nicht direkt von vorn aufnehmen konnte, da ich den Lichtstrahl sonst abgedeckt hätte.
Da vollkommen unbekannt ist, welches Photon wo entlang fliegt – rechts oder links an dem Draht vorbei – verhalten sie sich wie Wellen, werden gebeugt und interferieren. Man spricht von der Welcher-Weg-Information, die man in diesem Fall nicht hat.
Nun kommt die Polarisationsfolie ins Spiel. Wir basteln einen Filter, der zur Hälfte aus vertikal gerichteter, zur Hälfte aus horizontal gerichteter Polfolie besteht (Abbildung 3). Dazu werden aus der Polfolie Quadrate ausgeschnitten (ich habe Abmessungen von 4 cm mal 4 cm genommen; 0,5 cm gehen rundum verloren für die Befestigung im Papprahmen) und mit Klebefilm so in einen Rahmen aus Pappe geklebt, dass sie um 90° gegeneinander verdreht sind. Dabei ist es egal, welches Quadrat in welche Richtung gedreht wird. (Der Papprahmen erleichtert die Handhabung während des Experimentes, da man die Polfolie nicht berühren sollte.) Die beiden Quadrate sollen genau aneinanderstoßen, sich aber nicht überlappen. Genau über dieser Grenzlinie zwischen den beiden Quadraten wird nun der Draht befestigt.
- Abb. 3 ¦ Polfilter

- Der Filter ist aus zwei Stücken Polarisationsfolie zusammengesetzt, die beide um 90° gegeneinander verdreht sind. Genau auf der Grenze zwischen beiden habe ich den Draht befestigt. Es handelt sich um Basteldraht, schwarz lackiert, etwa 0,3 mm dick.
Dieser Filter wird nun vor den Laser-Pointer gestellt und das Experiment wiederholt – es wird also wieder der Draht mit dem Laser-Pointer bestrahlt (Abbildung 4). (Da der Laser-Pointer selbst auch polarisiertes Licht aussendet, muss noch ein 45°-Filter in den Strahl gestellt werden. Das vom Laser ausgehende Licht geht je nach Polarisationswinkel zu einem bestimmten Anteil hindurch. Nach Verlassen des 45°-Filters ist das hindurchgehende Licht in eben dieser 45°-Richtung polarisiert; steht also in einem 45°-Winkel sowohl zum horizontalen als auch zum vertikalen Polfilter.)
Betrachtet man nun den Schirm, vermisst man die Interferenzstreifen – sie sind verschwunden. Nur eine helle Fläche ist zu sehen (Abbildung 5). Deren Ausdehnung entspricht der Ausdehnung, die vorher das Streifenmuster hatte.
- Abb. 4 ¦ Versuchsaufbau II

- Der Versuchsaufbau mit dem 45°-Filter sowie dem aus zwei Polfolien zusammengesetzten Filter und dem Draht.
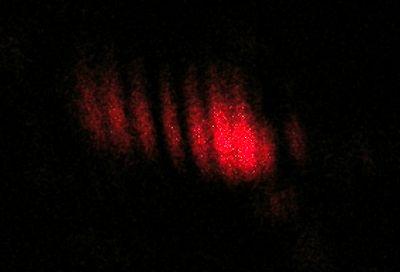
- Abb. 5 ¦ Lichtflecken hinter dem Draht

- Befinden sich um 90° gegeneinander verdrehte Polarisationsfilter im Strahl, verschwinden die Interferenzstreifen.
Was ist da passiert? Die Polarisationsfolie sorgt dafür, dass rechts neben dem Draht nur vertikal polarisiertes Licht durchkommt, links nur horizontal polarisiertes (oder umgekehrt, das spielt keine Rolle). Es ist jetzt also prinzipiell möglich, zu erkennen, welches Photon auf welcher Drahtseite geflogen ist. Auch wenn wir in diesem Experiment nicht die technischen Möglichkeiten haben, das tatsächlich zu messen – wir könnten es prinzipiell tun. Das bedeutet, dass wir in diesem Fall die Welcher-Weg-Information haben (könnten). Und das reicht aus, um die Interferenz beiden gebeugten Teilwellen zu beseitigen. Allein die prinzipielle Kenntnis des Ortes (rechts oder links) genügt, um das Interferenzmuster des Doppelspalts zu vernichten.
Was aber sieht man nun stattdessen? Der Lichtfleck ist immer noch Teil eines Interferenzmusters, nämlich desjenigen des Einzelspalts. Wenn man genau hinsieht, erkennt man rechts und links des hellen Flecks weitere, sehr schwache Helligkeitsmaxima, wie im Interferenzmuster eines Einzelspalts zu erwarten wäre.
Wäre der Weg der Photonen durch die Polarisationsfilter wirklich exakt bestimmt, die Ortsunbestimmtheit also vollkommen beseitigt, erhielte man überhaupt kein Interferenzmuster mehr, sondern lediglich Flecke, wie sie auch entstehen würden, wenn Bälle zufällig verteilt rechts und links an einem Säule vorbei auf eine Wand fliegen würden. (Wenn der Platz matschig und die Bälle entsprechend schmutzig wären.) Da aber bei der Beugung am Draht genügend Ortsunbestimmtheit übrig bleibt, entsteht weiterhin ein Interferenzmuster, nämlich das des Einzelspalts. Insofern kann das Experiment Photonen dann doch nicht als „echte“ Teilchen beobachtbar machen. Dennoch zeigt es den Einfluss der Unbestimmtheiten auf die Eigenschaften, die ein Quantenobjekt zeigt.
Nach dem Babinetschen Prinzip haben das Interferenzmuster einer Blende und das eines Gegenstandes in gleicher Form dieselbe Form – das Interferenzmuster einer Spaltblende ist also das gleiche wie das eines Drahtes gleicher Dicke. Allerdings gilt dies nur außerhalb des Bereiches, der durch die rein geometrische Abbildung entsteht. Das erklärt die dunkle „Taille“ des Einzelspaltmaximums in Abb. 5 – diese entsteht durch den Schatten des Drahtes.
Nun kann man aber noch etwas ganz Verrücktes tun – man kann diese Kenntnis des Ortes (der Welcher-Weg-Information) wieder vernichten. Dazu muss man einen weiteren Polfilter in den Strahl stellen, und zwar einen 45°-Filter (Abbildung 6). Dieser lässt sowohl von dem Licht, das durch den vertikalen Polfilter lief, wie auch von dem, das durch den horizontalen Filter lief, jeweils 50 Prozent durch. Hinter dem 45°-Filter sind beide Anteile in 45°-Richtung polarisiert und somit nicht mehr zu unterscheiden – man kann nicht mehr feststellen, ob ein bestimmtes Photon rechts oder links neben dem Draht vorbeigelaufen ist. Die Information über den Weg (rechts oder links?) ist nicht mehr vorhanden und das Licht sollte wieder das Interferenzmusters des Doppelspaltes zeigen. Und genau das passiert tatsächlich – dieses Interferenzmuster erscheint wieder! (Abbildung 7)
- Abb. 6 ¦ Versuchsaufbau III

- Der Versuchsaufbau mit dem 45°-Filter, dem aus zwei Polfolien zusammengesetzten Filter und dem Draht sowie dem zweiten 45°-Filter.
- Abb. 7 ¦ Wieder aufgetauchtes Beugungsbild

- Ein zusätzlicher 45°-Filter lässt das Interferenzmuster wieder auftauchen. (Das Beugungsbild war nach Durchgang durch insgesamt drei Polfilter sehr viel lichtschwächer als das in Abbildung 2. Es musste im Bildbearbeitungsprogramm GIMP deutlich aufgehellt werden; mit bloßem Auge war es nur schwer zu erkennen.)
Beugung am Draht – Einfachspalt oder Doppelspalt?
Eins hat mich zunächst verwirrt – im Experiment interferieren zwei Strahlen miteinander, der rechts am Draht vorbeilaufende und der links vorbeilaufende. Im Grunde entspricht das Ganze also der Beugung am Doppelspalt. So sieht das Beugungsbild auch aus (Abbildung 2). Man sieht (fast) gleich helle Maxima über eine begrenzte Ausdehnung, die der Breite des nullten Maximums des Einfachspalt-Beugungsbildes entspricht (siehe Beugung und Interferenz). Nach dem Babinetschen Theorem sollte das Beugungsbild eines Drahtes ja aber demjenigen eines Einfachspaltes entsprechen – die feine Unterteilung, die vom Doppelspalt herrührt, sollte also nicht auftreten.
Das Entscheidende ist das Verhältnis zwischen Spaltbreite b und Spaltabstand s. Ein klares Beugungsbild eines Doppelspaltes (beziehungsweise generell eines Mehrfachspaltes) erhält man nur, wenn der Spaltabstand groß gegen die Spaltbreite ist (siehe auf der Seite Beugung und Interferenz). Der Abstand der beiden Spalten des Doppelspaltes entspricht im Experiment hier der Dicke des Drahtes. Die einzelnen Spalte sind so breit wie das, was vom Lichtstrahl rechts und links am Draht vorbeiläuft. Mit einem dünneren Draht würde s also kleiner und b größer, das Verhältnis von Spaltabstand zu Spaltbreite also ungünstiger. In Abbildung 8 auf der Seite Beugung und Interferenz war das Bild des Einfachspaltes das Dominierende. In der Abbildung 8 war zwar der Draht genauso dick, es wurde aber keine Blende vor den Laser-Pointer gesetzt, so dass zwar s unverändert, b aber größer ist – was natürlich ebenfalls zur Folge hat, dass der Spaltabstand nicht mehr groß gegen die Spaltbreite ist.
In Abbildung 2 auf dieser Seite ist dagegen die Bedingung „Spaltabstand groß gegen Spaltbreite“ gut genug erfüllt, um ein Beugungsbild eines Doppelspaltes hervorzurufen.
Die Anzahl der vom Doppelspalt herrührenden Minima, die innerhalb des nullten Einfachspalt-Maximums zu sehen sind, ergibt sich übrigens als das Doppelte des Spaltabstandes s dividiert durch die Spaltbreite b: 2s/b. Mit kleinerem Spaltabstand (oder größerer Spaltbreite) treten weniger Doppelspalt-Minima auf, die Strukturierung des Einfachspaltbildes wird geringer. Was ja auch wieder nichts anderes heißt, als dass das Beugungsbild des Doppelspaltes in dasjenige eines Einfachspaltes übergeht. In Abbildung 8 auf der Seite Beugung und Interferenz gab es nur zwei Minima (auf dem Foto nicht zu erkennen) innerhalb des Einfachspalt-Hauptmaximums – im Gegensatz zu den zehn in Abbildung 2 auf dieser Seite.
(Das Beugungsbild des Fadens (Abbildung 9 auf Beugung und Interferenz) zeigte eine feinere, aber auch unregelmäßigere Struktur; ich vermute, dass die Tatsache, dass der Nylonfaden durchsichtig ist, hier noch kompliziertere Effekte zur Folge hat.)
© Wiebke Salzmann, August 2013
