Wellenfronten und ebene Wellen

Alle Punkte einer Welle, die sich im selben Schwingungszustand befinden – die also dieselbe Phase haben, bilden die so genannte Wellenfront. Beispielsweise bilden alle Punkte der Welle, die sich im gleichen (!) Maximum befinden, eine Wellenfront. Die Ausbreitungsrichtung der Welle ist senkrecht zu den Wellenfronten gerichtet.

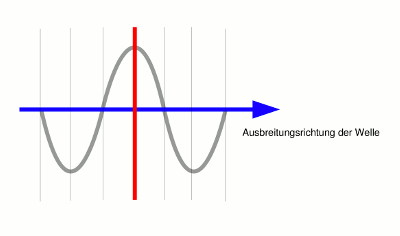
  Abb. 1 ¦ Phasen einer Welle  

Bildunterschrift Die Phase ist der Schwingungszustand einer Welle – hier sind der 1., 2., 3. und 4. Nulldurchgang, das 1. und 2. Minimum sowie das Maximum gekennzeichnet. Aber natürlich entspricht auch jeder beliebige Schwingungszustand dazwischen einer bestimmten Phase.
Eine Wellenfront würden beispielsweise alle Punkte des Maximums bilden, oder des 1. Minimums, oder alle Punkte des 2. Nulldurchganges – und so weiter.Bildunterschrift Ende

In einer ebenen Welle sind die Wellenfronten Ebenen und alle zueinander parallel. Auf solche ebenen Wellen beschränken wir uns im Folgenden. (Warum wir das tun, sehen wir dann noch.)
Jeder Punkt auf einer Wellenfront ist Ausgangspunkt einer neuen Welle, einer so genannten Elementarwelle. Eine Elementarwelle geht von einem Punkt aus und breitet sich kugelfömig aus. Die vielen Elementarwellen, die auf diese Weise von der Wellenfront ausgehen, überlagern sich und in der Summe ergibt sich genau die ursprüngliche Wellenfront – in unserem Fall also die parallelen, ebenen Fronten der ebenen Welle.

Beugung – wie kommt sie zustande?

Trifft eine solche ebene Welle auf ein Hindernis, wird die Wellenfront durch dieses Hindernis teilweise aufgehalten. Man sieht das zum Beispiel an dem Schatten, den ein Gegenstand wirft – hier konnte das Licht nicht hinter den Gegenstand gelangen. Allerdings ist ein Gegenstand, der für Licht ein Hindernis darstellt, nicht unbedingt eines für Schall – hinter einem Baum ist Schatten; das Geräusch eines davorstehenden Radios wird jedoch nicht abgeschirmt. Anders sieht es bei einem Haus aus – dieses wirft auch für den Schall einen Schatten. Das hat mit der Größe der Wellenlänge zu tun – je größer diese ist, desto größer muss das Objekt sein, um einen Schatten werfen zu können. Anders ausgedrückt – bei kleineren Gegenständen kann die Welle offenbar in den Schatten eindringen. Und zwar dann, wenn die Größe des Gegenstandes in der Größenordnung der Wellenlänge liegt. Wie kommt es nun zu dem Eindringen in den Schattenbereich?

Trifft eine (ebene) Wellenfront auf ein (kleines) Hindernis, verlaufen die Strahlen im Bild der Strahlenoptik einfach an den Rändern des Hindernisses geradlinig vorbei (Abbildung 2).
Wie wir eben behauptet haben, entspricht dieses Bild aber nicht der Erfahrung, sondern wir müssen die Wellenoptik bemühen. In der Wellenoptik müssen wir die Elementarwellen betrachten, die von der Wellenfront ausgehen und im ungestörten Zustand in der Überlagerung die ebene Wellenfront bilden. Da nun aber durch das Hindernis ein Teil der Wellenfront fehlt und damit auch ein Teil der Elementarwellen, ergibt deren Überlagerung an den Rändern des Hindernisses keine ebene Welle mehr. Dadurch krümmt sich die Wellenfront hinter dem Hindernis, wodurch sich hier auch die Ausbreitungsrichtung der Wellen ändert (diese steht ja senkrecht auf der Wellenfront). Es fällt nun auch Licht (oder Schall) in den Schatten. Diese Änderung der Ausbreitungsrichtung an Hindernisrändern nennt man Beugung.

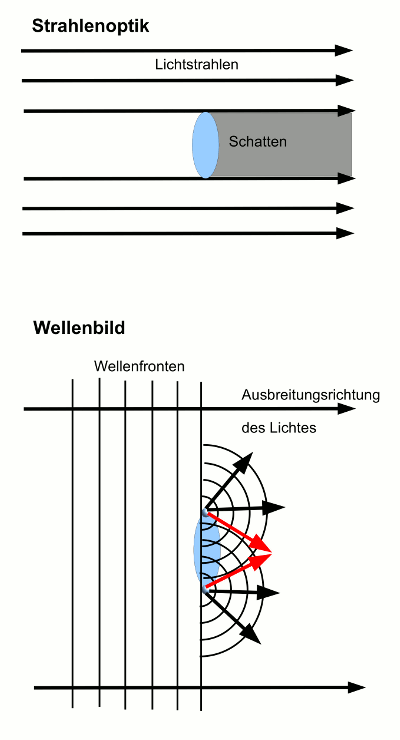
  Abb. 2 ¦ Licht trifft auf ein Hindernis  

Bildunterschrift Hindernisse im Strahlenbild und im Wellenbild – stark schematisch (und ohne Berücksichtigung von Interferenz)

In der Strahlenoptik (oben) blendet ein Hindernis (blauer Kreis) einen Teil des Strahls einfach aus – es wirft einen Schatten (grauer Bereich). An den Hindernisrändern laufen die Strahlen geradlinig in der ursprünglichen Ausbreitungsrichtung vorbei.

In der Wellenoptik (unten) werden die Punkte auf den Wellenfronten neben den Hindernisrändern zu Ausgangspunkten neuer Elementarwellen, die sich kugelförmig ausbreiten. Die Wellenfront krümmt sich und entspricht nur noch in einiger Entfernung vom Hindernis derjenigen einer ebenen Welle. Entsprechend ändert sich auch die Ausbreitungsrichtung des Lichtes an den Hindernisrändern – diese steht senkrecht zur Wellenfront, ist in einer Kugelwelle also radial gerichtet. So breiten sich auch Wellen in den Bereich hinter dem Hindernis aus (rote Pfeile).Bildunterschrift Ende

Je kleiner das Hindernis und je größer die Wellenlänge ist, desto eher muss man Beugungserscheinungen berücksichtigen. Die Strahlenoptik gilt streng eigentlich nur dann, wenn die Wellenlänge null ist oder das Hindernis unendlich groß. Erst dann gibt es überhaupt keine Beugungserscheinungen mehr. Aber in der Praxis braucht man nicht immer ganz so streng zu sein und kann die Beugungserscheinungen häufig vernachlässigen.

Beugungserscheinungen

Beugung führt nicht nur dazu, dass Licht in den Schattenbereich hinter einem Hindernis fällt, sondern kann unter bestimmten Umständen – zusammen mit der Interferenz – zu ganz besonderen Beugungserscheinungen führen – nämlich dann, wenn das einfallende Licht eine ebene Welle darstellt.
Dazu müssen wir uns zunächst ansehen, was passiert, wenn sich zwei Wellen überlagern.

Interferenz

Mit Interferenz sind die Erscheinungen gemeint, die die Überlagerung von zwei (oder mehr) Wellen mit sich bringt, wenn diese sich an einem Ort treffen. Die jeweiligen Auslenkungen der einzelnen Wellen an diesem Ort addieren sich – das heißt, das Aufeinandertreffen zweier Wellenberge führt zu einer größeren positiven Auslenkung; treffen ein Wellenberg und ein betragsmäßig größeres Wellental aufeinander, ergibt sich insgesamt eine kleinere negative Auslenkung und so weiter. Haben zwei aufeinandertreffende Wellen gleiche Amplituden und gleiche Frequenz und sind die Wellen so gegeneinander verschoben, dass die Wellenberge der einen mit den Wellentälern der anderen zusammentreffen, löschen sich beide Wellen aus. Ob die Überlagerung zweier Wellen zu Abschwächung oder Verstärkung führt, hängt daher davon ab, wie weit die Wellenzüge gegeneinander verschoben sind – diese Verschiebung nennt man Gangunterschied oder Phasenunterschied.
Interferenz tritt nicht nur bei Lichtwellen auf, sondern bei allen Wellen, so auch Wasser- oder Schallwellen.

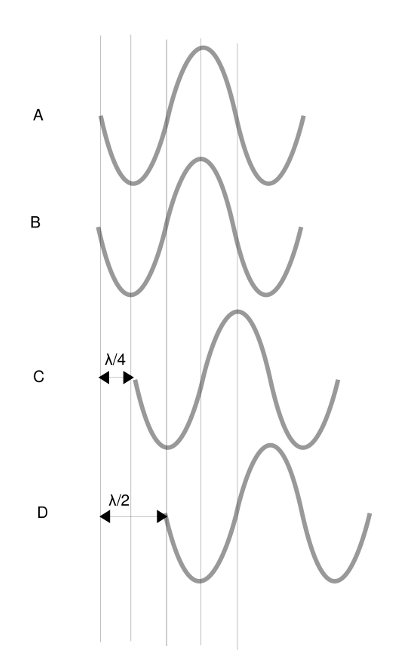
  Abb. 3 ¦ Phasenverschiebung  

Bildunterschrift Die Phasenverschiebung gibt an, wie weit Punkte gleicher Phase zweier Wellen gegeneinander verschoben sind.

Dargestellt sind hier Wellen gleicher Frequenz und gleicher Amplitude.
Die beiden Wellen A und B sind gar nicht gegeneinander verschoben, sie haben die Phasenverschiebung 0. (Sie könnten auch um eine ganze Wellenlänge λ gegeneinander verschoben sein, das wäre nicht zu erkennen.) Bei einer Überlagerung dieser beiden Wellen würde sich die Amplitude verdoppeln, es käme zur maximalen Verstärkung der Welle.
Die Wellen A und C sind um eine Viertelwellenlänge λ/4 gegeneinander verschoben – Nulldurchgänge von C treffen mit Minima und Maxima von A zusammen.
Die Wellen A und D sind um eine halbe Wellenlänge λ/2 gegeneinander verschoben, hier treffen Minima von A auf Maxima von D. Bei einer Überlagerung dieser beiden Wellen käme es zur Auslöschung.Bildunterschrift Ende

Die Überlagerung zweier Wellen lässt die Wellen selbst unverändert. Treffen ein Maximum und ein Minimum aufeinander, ist die Auslenkung an diesem Ort null, die Wellen löschen sich an diesem Ort aus. Beide wandern jedoch ungestört weiter, als wäre nichts passiert.

  Abb. 4a ¦ Interferenz von Wasserwellen I  

Bildunterschrift Auf dem ruhigen, dunklen Wasser dieses Teiches im Moor bei Graal-Müritz kann man sehr schön sehen, wie die Wellen – hervorgerufen durch das Fallen von Wassertropfen von den umstehenden Bäumen – sich überlagern, ohne sich gegenseitig zu beeinflussen. Die einzelnen Ringe setzen ihren Weg unbeeindruckt fort.Bildunterschrift Ende

  Abb. 4b ¦ Interferenz von Wasserwellen II  

Bildunterschrift Das untere Bild zeigt einen Wellenbrecher am Strand von Usedom. Der lange Steinwall weist mehrere Unterbrechungen auf, im Bild ist rechts vom Wall eine dieser Lücken zu sehen. Auf der linken Seite ist auch eine solche Lücke, wenn auch im Bild nicht sichtbar. Diese beiden Lücken wirken für die heranrollenden Ostseewellen wie ein Doppelspalt im unter Beugung am Doppelspalt beschriebenen Versuch. Man sieht schön die beiden Kreiswellen, die sich ausgehend von den Lücken Richtung Strand ausbreiten und ungestört überlagern.Bildunterschrift Ende

Interferenzmuster

In Abbildung 2 sind die von den Hindernisrändern ausgehenden Kugelwellen gezeichnet. Diese überlagern sich. An welchen Orten es dabei zur Verstärkung, Abschwächung oder gar Auslöschung kommt, hängt davon ab, wie groß der Phasenunterschied zwischen beiden Wellen an eben diesen Orten ist. Das wiederum hängt davon ab, wie lang der Weg ist, den beide Wellen von ihrem Ursprungsort zurücklegen mussten bis zum Ort der Überlagerung. Es entsteht so ein Muster aus hellen und dunklen Bereichen, das sichtbar wird, wenn man einen Schirm in das Licht hinter dem Hindernis hält.
Ist das Hindernis ein Draht, entsteht ein Streifenmuster, bei einer Kreisscheibe ein Muster aus konzentrischen Ringen. Um das Entstehen dieses Interferenzmusters genauer zu verstehen, nehmen wir statt eines Hindernisses eine Blende.

Beugung am Spalt und an der Blende I (Prinzip)

Fällt Licht durch einen schmalen Spalt oder eine kleine Blende, kommt es ebenfalls zur Beugung (Beugung tritt immer auf, wenn Licht auf Kanten fällt). Das führt dazu, dass beispielsweise auf einem Schirm die Blende nicht in ihrer wahren Ausdehnung abgebildet wird, sondern ein breiteres Bild entsteht. Das Licht wird an den Rändern der Blende gebeugt, und zwar auch nach außen (analog zu Abbildung 2), und fällt daher in einem größeren Bereich auf den Schirm. Handelt es sich um ebene Lichtwellen, entstehen auch hier Interferenzmuster – bei einem Spalt Interferenzstreifen, bei einer Kreisblende Ringe.

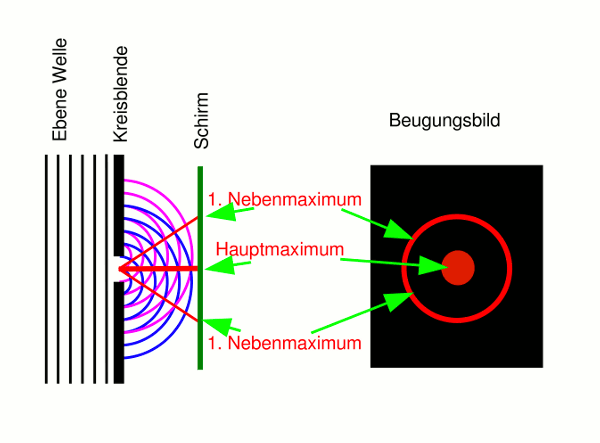
  Abb. 5 ¦ Beugung an einer Kreisblende  

Bildunterschrift Ebene Welle trifft auf eine Kreisblende.

Die Linien und Kreisbögen symbolisieren die Wellenberge. An Schnittpunkten von Kreisbögen addieren sich Wellenberge zu Intensitätsmaxima. Diese sind durch Linien verbunden, die die Lage der Intensitätsmaxima andeuten.
(Die Abbildung dient zur Veranschaulichung des Prinzips der Entstehung von Interferenzmustern. Die Beschränkung auf nur zwei Elementarwellen ist beim einfachen Spalt eigentlich nicht ausreichend. Dazu mehr im Abschnitt „Beugung am Spalt II“.)Bildunterschrift Ende

In Abbildung 5 sind die Wellenfronten zweier Elementarwellen gezeichnet, und zwar aus Gründen der Übersichtlichkeit nur die Wellenfronten, die zu den Wellenbergen gehören.
Die Schnittpunkte der Wellenfronten ergeben zwar alle eine Intensitätsverstärkung, gehören aber zu unterschiedlichen Ordnungen. Beispielsweise überlagern sich in der Mitte jeweils zwei Wellen gleichen „Alters“, beide wurden gleichzeitig ausgesandt, der Phasenunterschied zwischen beiden beträgt also null Wellenlängen. Alle diese Maxima nullter Ordnung sind durch eine Linie verbunden.
Diese Linie darf man ungestraft durchziehen, da eben nicht nur die Wellenberge sich addieren, sondern auch die anderen Phasen dazwischen – man muss sich für jede der beiden Wellen lauter Wellenfronthalbkreise für jede Phase zwischen den Wellenbergen vorstellen, die sich mit der entsprechenden Front der jeweils anderen Welle überlagern. Und für alle Schnittpunkte im Zentrum (auf der dicken roten Linie) gilt, dass der Phasenunterschied zwischen den beiden Wellen null beträgt.
Die Linie gibt also gewissermaßen die Ausbreitungsrichtung des nullten Intensitätsmaximums an. Hält man einen Schirm in den Strahl, wird man an der Stelle, wo die rote Linie ihn trifft, Helligkeit haben.
Auf dieselbe Weise verdeutlichen die dünneren roten Linien das 1. Nebenmaximum. Hier treffen zwei Wellen aufeinander, die einen Phasenunterschied von einer Wellenlänge haben. Im „oberen“ Nebenmaximum trifft die „zweite“ blaue Welle von unten auf die „erste“ rosa Welle von oben. Der Weg für die blaue Welle ist länger, nämlich genau eine Wellenlänge – was beim Aufeinandertreffen der Wellen den Phasenunterschied von einer Wellenlänge zur Folge hat. (Im „unteren“ Nebenmaximum gilt das entsprechende.)
Weiter außen liegen entsprechend Nebenmaxima höherer Ordnung, anders ausgedrückt: Intenstitätsmaxima, bei deren Entstehung sich Wellen immer größerer Phasenunterschiede überlagern.
Zwischen den Intensitätsmaxima liegen Intensitätsminima – hier beträgt der Phasenunterschied zwischen den beiden interferierenden Wellen eine halbe Wellenlänge (beziehungsweise ein ungerades Vielfaches wie 3/2, 5/2, …) und ein Schirm zeigt Dunkelheit.

Abbildung 5 dient zur Veranschaulichung des Prinzips der Entstehung von Interferenzmustern. Die Beschränkung auf nur zwei Elementarwellen ist beim einfachen Spalt nicht ganz korrekt. Dazu mehr im Abschnitt „Beugung am Spalt II“

  Abb. 6 ¦ Beugungsbild einer Kreisblende  

Bildunterschrift Dieses Beugungsbild wurde mit einem Laser-Pointer erzeugt. Den Pointer habe ich mit Alufolie umwickelt und in diese mit einer Nadel ein Loch gestochen. Dieses Loch wirkt als Kreisblende und erzeugt auf einem Schirm die konzentrischen Ringe des Beugungsbildes. (Die Ringe sind wirklich kreisförmig – so verzerrt sieht es nur aus, weil ich das Beugungsbild schräg von der Seite fotografieren musste, um nicht den Lichtstrahl zu verdecken.)Bildunterschrift Ende

  Abb. 7 ¦ Beugungsbild eines Spaltes

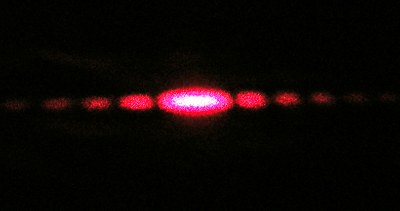
BildunterschriftDen Spalt habe ich einfach gebastelt, indem ich zwei Pappstücke sehr nah zusammengeschoben und mit Klebefilm fixiert habe. Beleuchtet habe ich mit einem Laser-Pointer. Bildunterschrift Ende

Ein Schirm im Lichtweg hinter der Blende ist also nicht mehr oder weniger gleichmäßig hell, sondern zeigt ein Interferenzmuster aus hellen und dunklen Bereichen. Dessen Form ist von der Form der Blende abhängig – ein Spalt erzeugt ein Streifenmuster, eine Kreisblende konzentrische Kreise (wie in Abbildung 6 und 7). Im Zentrum des Beugungsbildes herrscht Helligkeit, hier ist das Hauptmaximum der Intensität. Dieses stellt das Zentralbild der Blende dar – stark verbreitert. Daneben reihen sich die Nebenmaxima der Intensität auf, getrennt durch die Minima. Die Helligkeit der Nebenmaxima nimmt mit zunehmender Ordnung rasch ab. (Also je weiter weg ein Maximum vom Hauptmaximum liegt, desto dunkler ist es.)

In geringer Entfernung hinter der Blende beziehungsweise hinter dem beugenden Hindernis ist die Intensitätsverteilung kompliziert und hängt stark von der Entfernung zum beugenden Gegenstand ab. Erst in großer Entfernung geht die Intensitätsverteilung in das hier beschriebene Beugungsbild über. (Man spricht im ersten Fall von Fresnelscher Beugung, im zweiten Fall von Fraunhoferscher Beugung.)

Nach dem Babinetschen Theorem sind die Beugungsbilder zweier komplementärer beugender Gegenstände (fast) gleich. Das Beugungsbild einer Kreisscheibe ist also das gleiche wie das einer Kreisblende gleicher Größe.

  Abb. 8 ¦ Beugungsbild hinter einem Draht

BildunterschriftDer Draht ist 0,3 mm dick; es handelt sich um schwarz lackierten Basteldraht. Beleuchtet habe ich mit einem Laser-Pointer. Die Maxima sind strukturiert, bestehen aus feinen Streifen, was hier auf dem Foto nicht zu erkennen ist. Es fand also offenbar noch etwas statt, was wie Beugung am Doppelspalt wirkte. (Siehe dazu Abbildung 16 und Beugung und Welle-Teilchen-Dualismus) Bildunterschrift Ende

  Abb. 9 ¦ Beugungsbild hinter einem Faden

BildunterschriftBei dem Faden handelt es sich um Nägarn aus Nylon. Beleuchtet habe ich mit einem Laser-Pointer. Die Maxima sind strukturiert, bestehen aus feinen Streifen, was hier auf dem Foto nicht zu erkennen ist. Es fand also offenbar noch etwas statt, was wie Beugung am Doppelspalt wirkte. (Siehe dazu Abbildung 16 und Beugung und Welle-Teilchen-Dualismus) Bildunterschrift Ende

Beugung am Spalt II (Beugung am Einfachspalt)

Aufmerksamen Lesern wird aufgefallen sein, dass ich festgestellt habe, jeder Punkt der Wellenfront sei Ausgangspunkt einer neuen Elementarwelle, dann aber in Abbildung 5 nur zwei Elementarwellen gezeichnet habe. Dabei ist zu erwarten, dass zwischen diesen über der ganzen Breite des Spaltes noch mehr Elementarwellen auftreten. Um die Beugung am Einfachspalt korrekt zu beschreiben, muss man diese auch berücksichtigen.
Da die Ausbreitungsrichtung einer Welle senkrecht zur Wellenfront steht, ist sie bei kreisförmigen (oder besser: kugelförmigen) Fronten radial gerichtet (siehe Abbildung 2). Fasst man nun jede Ausbreitungsrichtung als eigenen Wellenzug auf, gibt es eine Welle für jeden Winkel (die Pfeile in Abbildung 2 sind also jeweils als Welle aufzufassen). Hat man nun viele Elementarwellen innerhalb des Spaltes, gibt es zu jedem Ablenkwinkel viele Wellenzüge – von jeder Elementarwelle einen.

  Abb. 10 ¦ Beugung am einfachen Spalt  

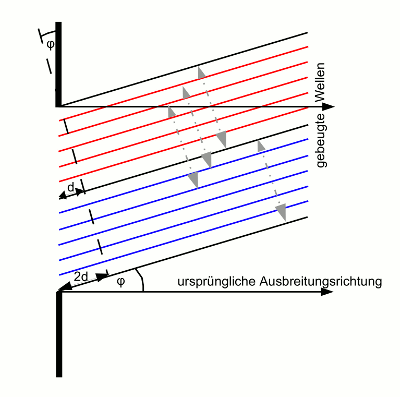
Bildunterschrift Gebeugte Wellen hinter dem Spalt, beispielhaft für einen Ablenkwinkel φ.

Bildunterschrift Ende

Das gebeugte Wellenbündel wird nun in zwei Hälften aufgeteilt (rot und blau in Abbildung 6; die schwarze Linie in der Mitte ist die Grenze zwischen beiden Wellenbündeln und gehört zu beiden; die anderen beiden schwarzen Linien stellen die Randstrahlen des Wellenbündels dar (korrekterweise müsste man eigentlich von „Randwellen“ sprechen).). Dabei beträgt der Phasenunterschied zwischen der ersten und der letzten Welle einer Hälfte jeweils d. Nun wird jeder Welle der oberen Hälfte die entsprechende der unteren Hälfte zugeordnet (graue Pfeile) – sodass der Phasenunterschied zwischen den Wellen eines Paares jeweils derselbe ist, und zwar d. Beträgt d nun eine halbe Wellenlänge, löschen sich alle Wellenpaare aus. Für den Ablenkwinkel φ, dem dieses d entspricht, herrscht auf einem Schirm also Dunkelheit.
Zu beachten ist dabei, dass der Phasenunterschied zweier sich auslöschender Wellen λ/2 beträgt – der Phasenunterschied zwischen den beiden Randstrahlen jedoch das Doppelte, nämlich λ. Immer dann, wenn der Phasenunterschied zwischen den Randstrahlen ein ganzzahliges Vielfaches der Wellenlänge ist, herrscht Dunkelheit.
Beim Ablenkwinkel 0° (also in der ursprünglichen Ausbreitungsrichtung) sind alle Wellen in Phase, der Phasenunterschied ist null und es entsteht das Hauptmaximum. Die Nebenmaxima liegen bei Ablenkwinkeln, bei denen der Phasenunterschied zwischen den Randstrahlen ein ungeradzahliges Vielfaches der halben Wellenlänge ist, also 3λ/2; 5λ/2; … (Bei λ/2 herrscht zwar Helligkeit, aber es handelt sich nicht um ein Maximum.)

  Abb. 11 ¦ Intensitätsverteilung hinter dem einfachen Spalt  

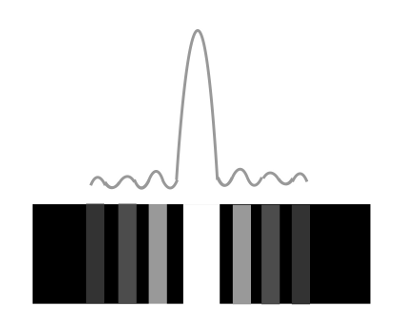
Bildunterschrift Schematische Darstellung der Intensitätsverteilung hinter einem einfachen Spalt (oben). Das Hauptmaximum ist doppelt so breit wie die Nebenmaxima und um ein Vielfaches ausgeprägter. Unten ist schematisch das Beugungsbild auf dem Schirm dargestellt.
Die berechnete Verteilung der Intensitäten finden Sie hier.
Bildunterschrift Ende

Darin ist Abbildung 5 mit der Beschränkung auf zwei Elementarwellen an den Rändern der Blende also nicht korrekt – denn hier entsteht Helligkeit, wenn der Phasenunterschied zwischen den beiden Randstrahlen ein Vielfaches der ganzen Wellenlänge ist. Das ist nur dann richtig, wenn es innerhalb des Spaltes tatsächlich nur zwei Elementarwellen gibt.
Für eine korrekte Darstellung muss man wie in Abbildung 10 sämtliche Elementarwellen berücksichtigen und sie in zwei Gruppen einteilen. Aber wenn ich das in Abbildung 5 gemacht hätte, könnte man das Licht vor lauter Wellen nicht mehr sehen …

Die Farbaufspaltung

Ob für einen bestimmten Ablenkwinkel Helligkeit oder Dunkelheit auf einem Schirm hinter einem Spalt herrscht, hängt vom Phasenunterschied der beteiligten Wellen ab. Dieser wiederum hängt davon ab, wie groß der Unterschied im zurückgelegten Weg (d in Abbildung 6) ist – und ob dieser ein Vielfaches der Wellenläge ist oder nicht. Was wiederum von der Wellenlänge abhängt – ein bestimmter Wegunterschied bedeutet für rotes Licht vielleicht einen Phasenunterschied von λ, für blaues aber nicht.
Die Ablenkwinkel, bei denen die Überlagerung zu Verstärkung der Lichtintensität, also zu einem hellen Streifen auf dem Schirm führt, sind daher für jede Wellenlänge andere. Somit liegen die Intensitätsmaxima und -minima – die Interferenzstreifen – auf einem Schirm für jede Farbe an einem anderen Ort. Benutzt man also weißes Licht für das Beugungsexperiment, entsteht für jede Farbe ein eigenes Interferenzmuster und das weiße Licht wird in seine Farben aufgespalten.
Nur im Hauptmaximum findet keine Trennung nach Farben statt – hier haben alle Farben Maxima, da alle hier den Phasenunterschied null haben.
Um die Bedingung 2d = 3/2λ zu erfüllen, erfordert eine größere Wellenlänge ein größeres d, also einen größeren Wegunterschied zwischen den beiden Randstrahlen. Ein größeres d bedeutet aber auch einen größeren Ablenkwinkel φ. Deshalb werden lange Wellen stärker abgelenkt als kurze – rotes Licht wird also stärker gebeugt als blaues. Die blauen Nebenmaxima liegen daher näher am Hauptmaximum als die roten.

Beugung am Doppelspalt

Fällt eine ebene Lichtwelle auf einen Doppelspalt, erzeugt jeder Einzelspalt eine neue Elementarwelle. Diese überlagern sich hinter dem Doppelspalt und erzeugen durch Interferenz ein Beugungsmuster aus hellen und dunklen Streifen auf einem Schirm. Die Intensitätsmaxima entstehen, wenn der Wegunterschied d zwischen den beiden Wellen ein ganzzahliges Vielfaches der Wellenlänge ist; die Minima für ungeradzahlige Vielfache der halben Wellenlänge.

  Abb. 13 ¦ Beugung am Doppelspalt I  

Bildunterschrift Bildunterschrift Ende

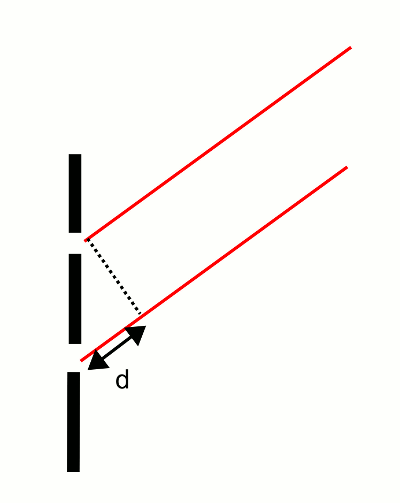
In der Darstellung mit Wellenfronten sieht das dann so aus, wie Abbildung 9 zeigt. Hier ist die Verwendung von zwei Elementarwellen wie in Abbildung 5 nun (zunächst) korrekt.

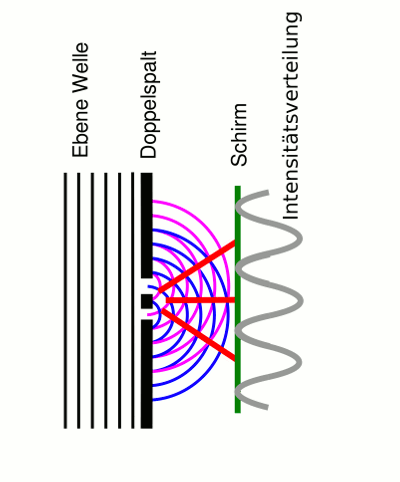
  Abb. 14 ¦ Beugung am Doppelspalt II  

Bildunterschrift Die Linien und Kreisbögen symbolisieren die Wellenberge. An Schnittpunkten von Kreisbögen addieren sich Wellenberge zu Intensitätsmaxima. Diese sind durch Linien verbunden, die die Lage der Intensitätsmaxima andeuten.
Die graue Kurve deutet die Intensitätsverteilung auf einem Schirm an. Bildunterschrift Ende

Verwendet man mehr Spalte als zwei, werden die Intensitätsmaxima enger und höher (ohne dabei ihre Lage auf dem Schirm zu ändern) und zwischen ihnen tauchen weitere, kleinere Maxima auf, deren Anzahl von der Anzahl der Spalte abhängt. Ein Beugungsgitter erzeugt entsprechend schmale, hohe Maxima. Da die Maxima für jede Farbe an einem anderen Platz liegen, kann ein Beugungsgitter genutzt werden, um Licht in seine Farben zu zerlegen. Beugungsgitter werden deshalb in Spektroskopen verwendet.

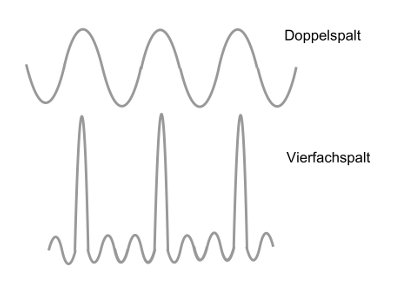
  Abb. 15 ¦ Intensitätsverteilung in Abhängigkeit von der Spaltenanzahl  

Bildunterschrift Je mehr Spalten beteiligt sind, desto enger und höher sind die Hauptmaxima und desto mehr Nebenmaxima treten zwischen diesen auf. (Bei einem Doppelspalt gibt es noch keine Nebenmaxima zwischen den Hauptmaxima.) Die Darstellung ist schematisch (und noch nicht die endgütige Wahrheit, siehe Abbildung 16).
Die berechnete Verteilung der Intensitäten finden Sie hier. Bildunterschrift Ende

Bisher haben wir so getan, als sende jeder Spalt nur eine Elementarwelle aus. In Wirklichkeit verhält sich aber natürlich jeder Spalt wie der oben besprochene Einfachspalt – das heißt, dem „Ein-Elementarwellen“-Beugungsmuster des Doppel-(oder Mehrfach-)spaltes überlagert sich dasjenige des Einfachspaltes. Das führt dazu, dass die Hauptmaxima nicht mehr alle gleich hoch sind.
Man kann genauso gut andersherum argumentieren – dem Beugungsbild des Einfachspaltes überlagert sich das des Doppelspaltes. Wo ein Einfachspalt Dunkelheit erzeugt, bleibt es auch dunkel – gleichgültig, wie viele Spalte noch zugefügt werden. Wo das Beugungsbild des Einfachspaltes jedoch Helligkeit erzeugt, kann die Interferenz des zugehörigen Strahles des einen Spaltes mit dem entsprechenden (also in den gleichen Ablenkwinkel gebeugten) Strahl des zweiten Spaltes dazu führen, dass aus Helligkeit Dunkelheit wird, weil diese beiden „hellen“ Strahlen sich nun auslöschen, wenn ihr Phasenunterschied eine halbe Wellenlänge beträgt. Die Maxima des Einfachspaltes sind daher unterbrochen von Minima des Doppelspaltes. Die Anzahl der Minima hängt ab von Spaltbreite und Spaltabstand.

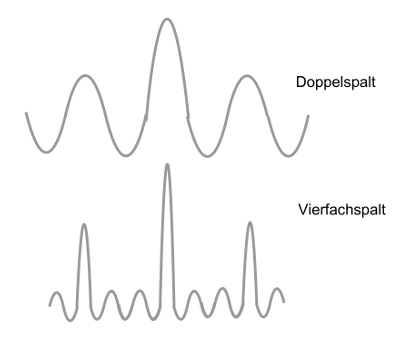
  Abb. 16 ¦ Intensitätsverteilung hinter dem Doppelspalt  

Bildunterschrift Das Beugungsbild des einfachen und des Doppelspaltes überlagern sich. Die Maxima des Doppelspaltes haben daher nicht alle dieselbe Höhe, wie in Abbildung 10 angenommen (oben). (Wenn Intensitätsmaxima nicht dieselbe Höhe haben, heiß das, das Licht ist verschieden hell.) Für Vierfachspalte gilt dasselbe (unten).
Die Darstellung ist schematisch.
Die berechnete Verteilung der Intensitäten finden Sie hier. Bildunterschrift Ende

  Abb. 17 ¦ Beugungsbild hinter dem Doppelspalt  

Bildunterschrift Das Beugungsbild (schematisch) des einfachen und des Doppelspaltes überlagern sich. In den Minima des Einfachspaltes treten keine Doppelspalt-Maxima auf; die Maxima des Einfachspaltes sind durch die Minima des Doppelspaltes in Streifen unterteilt. Bildunterschrift Ende