Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Intensitäten
Auf dieser Seite erwarten Sie intensive Berechnungen.
www.wissenstexte.de > Physik-Wissen > Optik > Beugung > Intensitätsverteilungen nach Beugung am Spalt
Verteilung der Intensitäten des Lichtes hinter einem Spalt
– Mehrfachspalt ohne Berücksichtigung der Einfachspalte
– Mehrfachspalt mit Berücksichtigung der Einfachspalte
– Spaltbreite und Spaltabstand
Wie sich die Lichtintensität hinter einem Spalt auf einem Schirm verteilt, lässt sich berechnen. Die Formeln dazu finden sich in Lehrbüchern. Mithilfe eines Tabellenkalkulationsprogramms (wie OpenOffice Calc) habe ich die unten abgebildeten Kurven berechnet; für eine Spaltbreite von 25 µm und eine Wellenlänge von 500 nm (sofern nicht anders angegeben). Auf der x-Achse ist der Winkel in Grad abgetragen, die Einheiten für die Intensität auf der y-Achse sind willkürlich.
- Formel zur Berechnung der Intensitätsverteilung hinter einem Einfachspalt
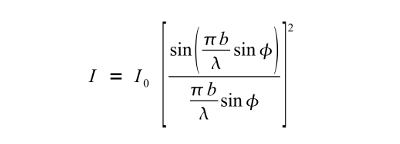
- Es bedeuten: I = Intensität des gebeugten Lichtes für einen bestimmten Beugungswinkel; I0 = Intensität für den Beugungswinkel 0°, also in der ursprünglichen Ausbreitungsrichtung; φ = Beugungswinkel; b = Spaltbreite; λ = Wellenlänge
- Formel zur Berechnung der Intensitätsverteilung hinter einem Mehrfachspalt
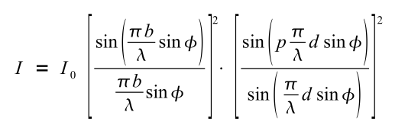
- Es bedeuten: I = Intensität des gebeugten Lichtes für einen bestimmten Beugungswinkel; I0 = Intensität für den Beugungswinkel 0°, also in der ursprünglichen Ausbreitungsrichtung; φ = Beugungswinkel; b = Spaltbreite; d = Abstand der Spalte; p = Anzahl der Spalte; λ = Wellenlänge
Die Formel hat zwei Faktoren – der Vergleich mit der Formel für den Einfachspalt zeigt, dass der erste Faktor die Intensitätsverteilung des Einfachspaltes darstellt. Da jeder Spalt des Mehrfachspaltes auch ein Einfachspalt ist und das Licht wie ein solcher beugt, wird das Beugungsbild des Mehrfachspaltes durch das des Einfachspaltes moduliert.
Auf der y-Achse der Abbildungen ist die Intensität aufgetragen (genauer gesagt: I/I0, ich habe in den Formeln oben also beide Seiten durch I0 dividiert). Dort, wo die Kurven einen positiven Ausschlag haben, fällt Licht auf den Schirm. Es ist umso heller, je größer der Ausschlag, also der y-Wert, der Kurve ist.
Auf der x-Achse ist der Beugungswinkel aufgetragen. Bei 0° wird das Licht gar nicht gebeugt, dieser Winkel entspricht also der ursprünglichen Ausbreitungsrichtung. Mit zunehmendem Beugungswinkel trifft das Licht immer weiter rechts auf den Schirm. Dargestellt ist nur die Hälfte der Beugungsbilder – eigentlich müssten sie für negative Winkel links von 0° erweitert werden, da die Beugung natürlich symmetrisch um die 0°-Richtung stattfindet. Da sich der Teil der Kurve aber durch einfache Spiegelung an der y-Achse ergibt, habe ich darauf verzichtet.
Einfachspalt
Bei der Beugung am Einfachspalt fällt das hohe Zentralmaximum bei einem Beugungswinkel um 0° auf; die Nebenmaxima bei größeren Beugungswinkeln sind im Gegensatz dazu sehr viel flacher. (Ein Beugungswinkel von 0° heißt natürlich, dass das Licht hier nicht oder wenig gebeugt wird, sondern der ursprünglichen Ausbreitungsrichtung folgt.)
(siehe auch: Beugung und Interferenz)
- Abb. 1 ¦ Einfachspalt
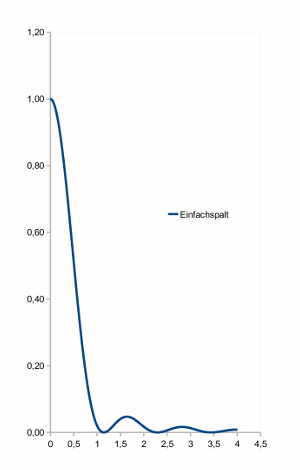
- Intensitätsverteilung bei der Beugung am Einfachspalt
x-Achse bis 4,5°
Mehrfachspalt
Mehrfachspalt ohne Berücksichtigung der Beugung am Einfachspalt
Die Formel zur Berechnung der Intensitätsverteilung hinter einem Mehrfachspalt enthält zwei Faktoren – der eine beschreibt die eigentliche Beugung am Mehrfachspalt, der andere die Beugung am Einfachspalt. Denn jeder einzelne Spalt ist für sich ja auch wieder ein Einzelspalt und die Beugung an einem solchen muss daher auch berücksichtigt werden.
(Siehe auch: Beugung und Interferenz)
Abbildung 2 zeigt zunächst die Beugung an einem Doppel- und einem Vierfachspalt ohne Berücksichtigung der Beugung am Einzelspalt. Neben den hohen Maxima gibt es auch noch kleinere Maxima – deren Anzahl ist gleich der Anzahl der Spalte minus 2. Deshalb gibt es beim Doppelspalt auch keine kleinen, sondern nur die hohen Maxima. In Abbildung 6 ist zu sehen, dass bei einem Achtfachspalt auch entsprechend sechs kleinere Maxima zwischen den hohen Maxima liegen.
Die hohen Maxima werden mit zunehmender Spaltenzahl höher, aber auch schmaler.
- Abb. 2 ¦ Mehrfachspalt ohne Einfachspalt
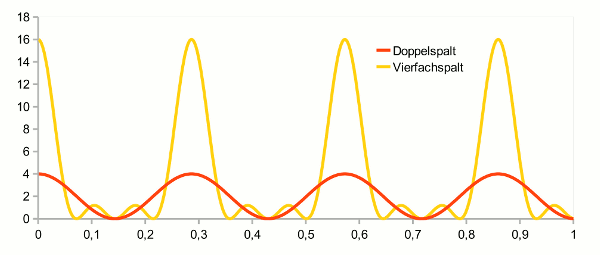
- Intensitätsverteilung bei der Beugung am Mehrfachspalt ohne Berücksichtigung der Beugung am Einfachspalt.
rot = Doppelspalt; gelb = Vierfachspalt; x-Achse bis 1°
Mehrfachspalt mit Berücksichtigung der Beugung am Einfachspalt
Führt man die Berechnung mit der vollständigen Formel durch, berücksichtigt also auch, dass jeder Spalt auch als Einzelspalt wirkt und entsprechende Beugungseffekte hervorruft, erhält man Abbildung 3. Am Auftreten von kleinen Maxima zwischen den hohen beim Vierfachspalt (und am Fehlen derselben beim Doppelspalt) hat sich nichts geändert. (Zu beachten ist, dass der Spaltabstand sehr viel größer als die Spaltbreite sein muss.)
- Abb. 3 ¦ Mehrfachspalt mit Einfachspalt
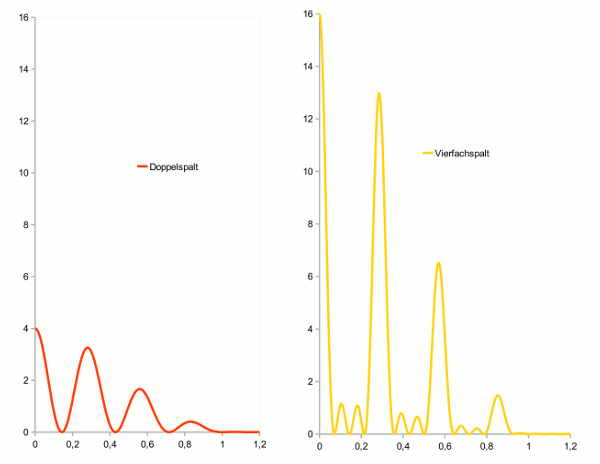
- Intensitätsverteilung bei der Beugung am Mehrfachspalt mit Berücksichtigung der Beugung am Einfachspalt.
rot = Doppelspalt; gelb = Vierfachspalt; x-Achse bis 1,2°; die Skalierung der y-Achse ist für beide Kurven gleich.
Während vorher alle hohen und alle kleinen Maxima jeweils gleich groß waren, nimmt die Höhe nun mit zunehmendem Beugungswinkel ab. Stellt man einen größeren Winkelbereich dar und vergleicht die Kurven der Mehrfachspalte mit der des Einfachspaltes, fällt auf, dass die Kurve des Einfachspaltes eine Hüllenkurve der Maxima der Mehrfachspalte zu sein scheint.
- Abb. 4 ¦ Mehrfachspalt und Einfachspalt
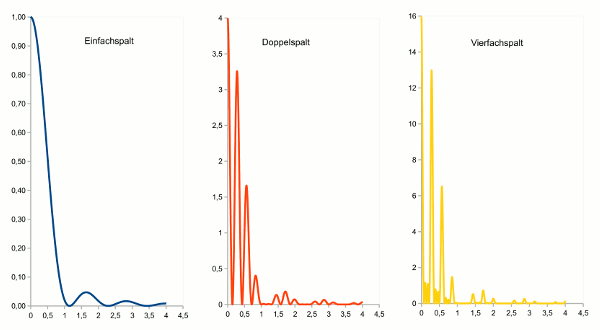
- Intensitätsverteilung bei der Beugung am Einfachspalt im Vergleich mit der Beugung am Mehrfachspalt. Die y-Achsen sind unterschiedlich skaliert, um die Maxima für den Vergleich der Kurvenform auf gleiche Höhe zu bringen.
blau = Einfachspalt; rot = Doppelspalt; gelb = Vierfachspalt; x-Achse bis 4,5°
Dass das tatsächlich so ist, sieht man, wenn man die Kurve des Einfachspaltes streckt und diese Kurve zusammen mit der des Mehrfachspaltes darstellt (hier beispielhaft für den Vierfachspalt).
Die Kurve muss gestreckt werden, da die maximal erreichten Intensitätswerte beim Einfachspalt kleiner sind als beim Mehrfachspalt. Natürlich ändert sich nichts an der Gesamtmenge Licht. Die Intensitätsmaxima sind beim Mehrfachspalt entsprechend schmaler; im Vergleich zum Beugungsbild des Einfachspaltes liegen unter einem „Einfachspalt-Maximum“ mehrere dunkle Streifen.
- Abb. 5 ¦ Einfachspalt als Hüllenkurve von Mehrfachspalt
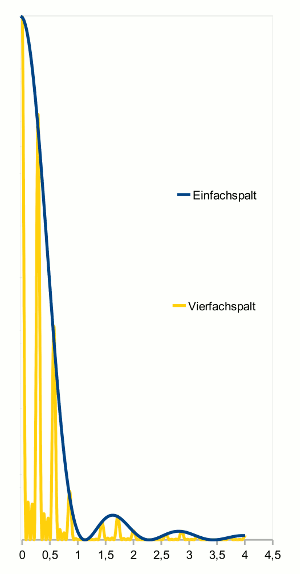
- Die Intensitätsverteilung des Einfachspaltes kann als Hüllenkurve (blau) derjenigen des Mehrfachspaltes (gelb) aufgefasst werden (nach entsprechender Streckung der y-Achse). x-Achse bis 4,5°
Wie oben schon erwähnt, nimmt die Höhe der hohen Maxima mit zunehmender Spaltenanzahl zu, gleichzeitig werden sie immer schmaler. Die kleinen Maxima werden zwar auch höher, aber trotzdem wird der Unterschied zwischen hohen und kleinen immer größer. Bei einem Beugungsgitter spielen sie aufgrund der hohen Spaltenzahl schließlich keine Rolle mehr. Abbildung 6 verdeutlicht dies noch einmal durch Hinzunahme eines Achtfachspaltes. (Die Anzahl der kleinen Maxima steigt hier auf 8 − 2 = 6.)
- Abb. 6 ¦ Verschiedene Spaltenanzahlen
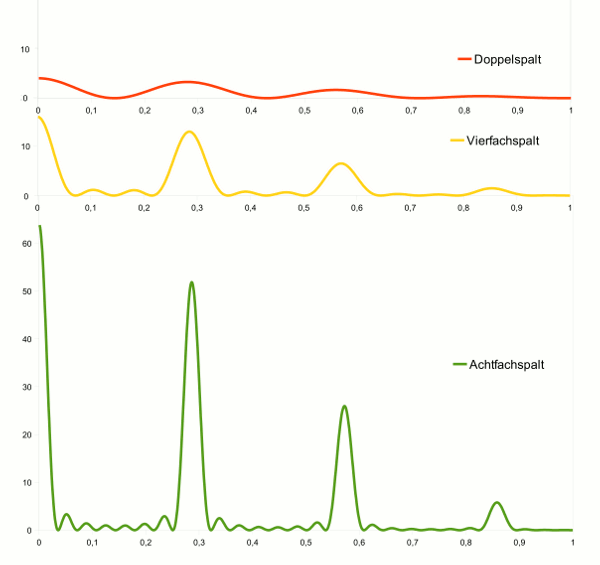
- Vergleich von Doppel-, Vierfach- und Achtfachspalt. Die Skalierung der y-Achse ist für alle drei Kurven dieselbe, um die Höhe der Maxima vergleichen zu können.
rot = Doppelspalt; gelb = Vierfachspalt; grün = Achtfachspalt; x-Achse bis 1°
Einfluss von Spaltbreite und Spaltabstand
Eine Erhöhung der Spaltbreite hat zur Folge, dass die Maxima der Kurve des Einfachspaltes (beziehungsweise der Hüllkurve beim Mehrfachspalt) enger werden.
- Abb. 7 ¦ Einfluss der Spaltbreite
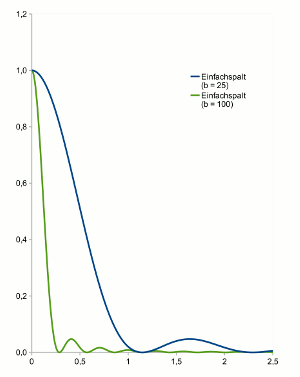
- Intensitätsverteilung hinter einem Einfachspalt.
Blau: Spaltbreite 25 µm; grün: Spaltbreite 100 µm; x-Achse bis 2,5°
Eine Erhöhung des Abstandes zwischen den Spalten hat zur Folge, dass die Maxima des Beugungsbildes des Mehrfachspaltes enger werden. Es treten nun in einem festen Winkelbereich mehr Maxima auf.
- Abb. 8 ¦ Verschiedene Spaltabstände
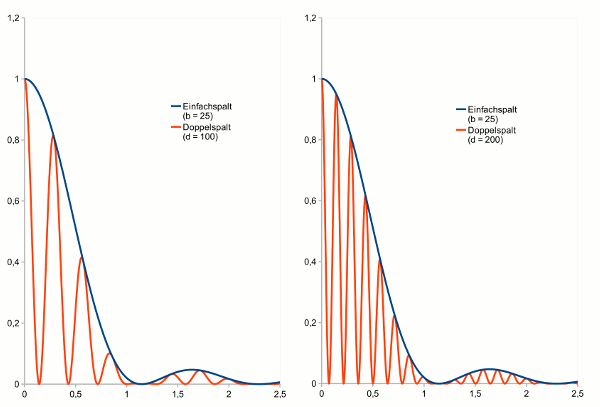
- Intensitätsverteilung hinter einem Doppelspalt. Links: Spaltabstand 100 µm, rechts: Spaltabstand 200 µm; die Hüllenkurve entspricht in beiden Fällen derjenigen für eine Spaltbreite von 25 µm; x-Achse bis 2,5°; die Kurven vom Doppelspalt sind gestaucht.
Oben wurde erwähnt, dass der Spaltabstand groß sein muss im Vergleich zur Spaltbreite. Abbildung 9 zeigt den Fall, dass der Spaltabstand mit 200 µm nur doppelt so groß ist wie die Spaltbreite von 100 µm. Die Hüllenkurve entspricht nach wie vor der Intensitätsverteilung hinter dem Einfachspalt von 100 µm. Da deren 1. Minimum aber mit dem zweiten Maximum der Kurve des Doppelspaltes trifft, wird dieses Maximum fast vollständig unterdrückt. Übrig bleiben nur zwei kleine positive Ausschläge rechts und links vom eigentlichen Maximum. Für größere Beugungswinkel ähnelt das Beugungsbild dann demjenigen des Einfachspaltes. Um das Beugungsbild des Mehrfachspaltes zu erhalten, muss die Bedingung, dass der Spaltabstand groß gegen die Spaltbreite sein muss, erfüllt sein.
Dass das zweite Maximum des Doppelspaltes durch das Minimum des Einfachspaltes unterdrückt wird, verdeutlicht, dass das Hinzufügen weiterer Spalten niemals an Stellen Helligkeit erzeugen kann, an denen das Beugungsbild des Einfachspaltes Dunkelheit liefert. Umgekehrt kann aber durchaus durch mehrere Spalten an einer Stelle Dunkelheit erzeugt werden, für die der Einfachspalt Helligkeit liefert.
- Abb. 9 ¦ Kleiner Spaltabstand
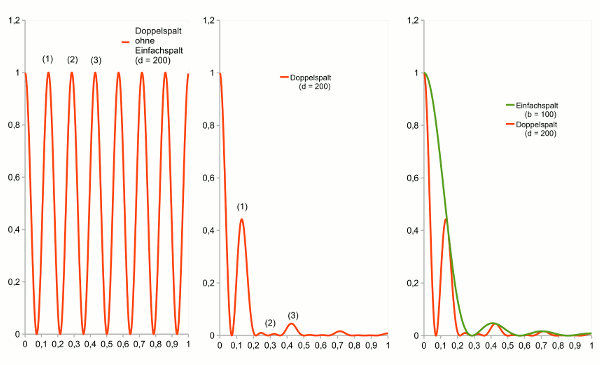
- Intensitätsverteilung hinter einem Doppelspalt; Spaltabstand 200 µm; Spaltbreite 100 µm. Links: ohne Berücksichtigung der Beugung am Einfachspalt; Mitte und rechts: mit Berücksichtigung der Beugung am Einfachspalt; rechts: mit Hüllkurve (Einfachspalt; grü). Drei Maxima im linken Bild und ihre Entsprechungen im mittleren Bild sind nummeriert; x-Achse bis 1°
In Abbildung 10 ist ein Beispiel zu sehen, in dem man die Auswirkungen direkt sieht. Allerdings ist hier nicht der Spaltabstand unterschiedlich groß, sondern die Spaltbreite. Aber die Bedingung, dass der Abstand der Spalte groß gegen ihre Breite sein muss, ist ja auch dann nicht erfüllt, wenn die Spaltbreite zu groß wird.
Diese Beugungsbilder wurden nicht mit einem Spalt, sondern mit einem Laser-Pointer und einem Draht gewonnen. (Der Draht ist 0,3 mm dick; es handelt sich um schwarz lackierten Basteldraht.) Der Abstand der beiden Spalten des Doppelspaltes entspricht im Experiment hier der Dicke des Drahtes. Die einzelnen Spalte sind so breit wie das, was vom Lichtstrahl rechts und links am Draht vorbeiläuft. Mit einem dünneren Draht würde der Spaltabstand also kleiner und die Spaltbreite größer. Oder man verwendet unterschiedlich große Lichtquellen. Genau das habe ich hier gemacht. In Abbildung 10 hatte der Laser-Pointer eine Blende aus Alufolie, in die ich mit einer Nadel ein Loch gestochen habe. Hier ist die Spaltbreite also klein (genug) gegen den Spaltabstand und es entsteht das Beugungsbild eines Doppelspaltes. Man sieht (fast) gleich helle Maxima über eine begrenzte Ausdehnung, die der Breite des nullten Maximums des Einfachspalt-Beugungsbildes entspricht. In Abbildung 11 dagegen ist das Bild des Einfachspaltes das Dominierende. Hier war zwar der Draht genauso dick, ich habe aber keine Blende vor den Laser-Pointer gesetzt, so dass die Spaltbreite größer ist. (Hier auf dem Foto ist es nicht zu sehen, aber auch auf diesem Bild gab es zwei Minima im Zentralmaximum, also noch „Reste“ des Beugungsbildes des Doppelspaltes.)
- Abb. 10 ¦ Doppelspalt-Beugungsbild hinter einem Draht

- Die Schiefe der Linien kommt daher, dass ich das Foto nicht direkt von vorn aufnehmen konnte, da ich den Lichtstrahl sonst abgedeckt hätte.
- Abb.11 ¦ Einfachspalt-Beugungsbild hinter einem Draht

© Wiebke Salzmann, August 2013
