Ideale Gase

Die drei Größen Druck P, Temperatur T und Volumen V eines Gases hängen voneinander ab. Als Gleichung hingeschrieben, sieht das so aus:

P V = n R T.

(Allerdings gilt das Gasgesetz in dieser Form streng genommen nur für ideale Gase, also solche, deren Teilchen nicht miteinander wechselwirken; die also auch nicht kondensieren. Man kann das Gesetz allerdings in weiten Bereichen auch für reale Gase anwenden.) R ist eine Konstante und heißt allgemeine Gaskonstante, n ist die Anzahl Mol (Mol ist eine Einheit, um die Menge eines Stoffes anzugeben).
Das Produkt aus Druck und Volumen ist also proportional zur Temperatur. Einige Spezialfälle lassen sich leicht verstehen:

1. Wenn man das Volumen eines Gases konstant hält

(beispielsweise, indem man es in einen Behälter füllt), wird die Gleichung zu:

P = n R T / V oder P ∼ T (zu lesen als: P ist proportional zu T).

Dann führt eine Erhöhung der Temperatur (also die Zuführung von Wärme) zu einer Zunahme des Druckes. Das liegt daran, dass eine Erhöhung der Temperatur die Gasmoleküle in schnellere Bewegung versetzt und sie mit höherer kinetischer Energie an die Wände des Behälters stoßen lässt. Diese Stöße der Moleküle – beziehungsweise der dabei auf die Behälterwand übertragene Impuls – sind aber genau das, was man makroskopisch als Druck wahrnimmt. Umgekehrt führt eine Erniedrigung der Temperatur zu einer Abnahme des Druckes.

2. Wenn man die Temperatur konstant hält,

wird die Gleichung zu:

P V = konstant,

das Produkt aus Druck und Volumen ist also konstant unter diesen Bedingungen. Wird das Gas nun einem höheren Druck ausgesetzt, verkleinert sich entsprechend sein Volumen. Umgekehrt führt eine Verkleinerung des Volumens zu einer Druckerhöhung. Zustandsänderungen bei konstanter Temperatur nennt man isotherm.

3. Hält man den Druck konstant,

gilt die Gleichung:

V = n R T / P oder V ∼ T.

Eine Temperaturerhöhung führt jetzt zu einer Volumenzunahme. Die sich schneller bewegenden Teilchen benötigen mehr Platz, deshalb dehnt das Gas sich aus. Um das zu verstehen, setzen wir das Gas gedanklich in einen flexiblen Behälter, der sich mit dem Gas ausdehnt. Würde sich das Gas nun nicht ausdehnen, würden die Teilchen heftiger an die Begrenzung stoßen, es käme zu einem größeren Impulsübertrag, also einem größeren Druck. Der soll ja aber unverändert bleiben, was durch die Volumenzunahme erreicht wird. Denn jetzt stoßen die Teilchen zwar auch mit größerer Geschwindigkeit an die Behälterwände, aber sie tun das seltener (wegen der größeren Entfernung). Auch eine geringere Häufigkeit von Stößen verringert den Impulsübertrag und damit auch den Druck wieder.
Bei einer Temperaturabnahme verringert sich das Volumen entsprechend. Zustandsänderungen bei konstantem Druck nennt man isobar.

Hierzu gibt es ein einfaches Experiment, das bei Zuschauern immer gut ankommt:

  Abb. 1 ¦ Einen Ballon in einer Flasche aufblasen  

BildunterschriftEine Flasche wird zunächst mit kochend heißem Wasser gefüllt und einige Minuten stehen gelassen. Hat die Flasche sich erhitzt, gießt man das Wasser wieder aus (Topfhandschuhe benutzen – die Flasche ist jetzt heiß!) und stülpt einen Luftballon über die Öffnung. Dann wartet man. Irgendwann plöppt der Ballon plötzlich in die Flasche und dehnt sich dort mehr und mehr aus. Wenn er nicht vorher platzt (was leider in etwa einem Drittel der Fälle passiert ist), kann er die Flasche bis zur Hälfte füllen (es handelte sich um eine 1-L-Flasche).

Versuchsanleitung hier:
Der Kinderbrockhaus – Erste Experimente für kleine Forscher. Christoph Michel, Bibliographisches Institut & F. A. Brockhaus AG, Mannheim, 2008.Bildunterschrift Ende

Erläuterung: Der Druck der Außenluft (der Luftdruck) bleibt während des ganzen Experimentes konstant.
Die Luft in der durch das heiße Wasser erhitzten Flasche ist zunächst heiß. Ihre Teilchen sind schneller und üben einen größeren Druck auf die Außenluft aus. Die „Flaschenluft“ dehnt sich also aus und verdrängt Luft aus der Flasche, das heißt, die Teilchenzahl in der Flasche nimmt ab. Und zwar so lange, bis die damit einhergehende Druckabnahme in der „Flaschenluft“ dazu geführt hat, dass der Druck der „Flaschenluft“ wieder dem Außenluftdruck entspricht.
Nun wird der Ballon über die Flasche gestülpt. Die „Flaschenluft“ kühlt allmählich ab. Dadurch werden ihre Teilchen langsamer und üben im ersten Moment weniger Druck auf die Außenluft aus. Oder andersherum ausgedrückt übt die Außenluft nun mehr Druck auf die „Flaschenluft“ aus. Die „Flaschenluft“ zieht sich zusammen (beziehungsweise die Außenluft dehnt sich in die Flasche hinein aus), die Dichte der „Flaschenluft“ steigt und die Anzahl Stöße nimmt zu, der Druck der „Flaschenluft“ erhöht sich – auf die Weise entspricht der Druck der „Flaschenluft“ während des Abkühlens ständig dem Luftdruck.
Der Druck der „Flaschenluft“ bleibt also während des ganzen Experimentes gleich – nämlich gleich dem Luftdruck – und somit hat die Abkühlung der „Flaschenluft“ eine Volumenabnahme zur Folge.
Die Außenluft folgt also der sich zusammenziehenden „Flaschenluft“ in die Flasche hinein. Da zwischen beiden der Ballon hängt, wird er ebenfalls von der Außenluft in die Flasche gedrückt beziehungsweise von der sich zusammenziehenden „Flaschenluft“ hineingesaugt – das hängt davon ab, ob man das Ganze aus Sicht der Außenluft oder der der „Flaschenluft“ betrachtet.

  Abb. 1b ¦ Luftdruck sichtbar gemacht  

BildunterschriftFüllt man ein Glas mit Wasser und legt ein Papier darüber, kann man das Glas auf den Kopf drehen, ohne dass das Wasser ausläuft. (Beim Drehvorgang selbst das Papier festhalten!) Der Außendruck (Luftdruck) hält das Wasser im Glas. Das Papier dient nur, um das Eindringen der Luft in das Glas zu verhindern. (Zur Sicherheit habe ich natürlich doch eine Schüssel unter das Experiment gestellt …).

Adiabatische Zustandsänderung

Die Luft in der Flasche kühlte ab – sie hat also Wärme an die Umgebung abgegeben. Das führt uns zu einem weiteren Spezialfall: der adiabatischen Zustandsänderung. Adiabatisch ist eine Zustandsänderung dann, wenn keine Wärme mit der Umgebung ausgetauscht wird. Das Gas (oder sonstige System) muß also thermisch völlig gegen die Umgebung isoliert sein. Annähernd adiabatisch sind aber solche Vorgänge, die so schnell ablaufen, daß praktisch kein Wärmeaustausch stattfinden kann. Beispielsweise kann der Verdichtungstakt beim Motor als adiabatische Kompression angesehen werden (siehe carnotscher Kreisprozess).
Die innere Energie eines idealen Gases hängt nur von seiner Temperatur ab, wobei man bei Temperaturen weit oberhalb des Kondensationspunktes auch reale Gase als ideal auffassen kann. Änderungen der inneren Energie kann man durch Zu- oder Abfuhr von Wärme oder Arbeit bewirken. Komprimiert man nun ein ideales Gas, führt man ihm Arbeit zu, erhöht also seine innere Energie. Komprimiert man es adiabatisch – also ohne Zu- oder Abfuhr von Wärme – ist diese Arbeitsverrichtung die einzige Änderung der inneren Energie. Die Temperatur des Gases/der Luft nimmt also zu.
Die adiabatische Expansion eines Gases führt entsprechend zu einer Abkühlung des Gases. Zum Beispiel wenn sich ein erhitztes Gas in einem Zylinder ausdehnt und dabei einen Kolben hinausdrückt. Dabei verrichtet es Arbeit an dem Kolben, die Energie dazu stammt aus der inneren Energie des Gases, die demzufolge abnimmt.
Bewegungsenergie der Teilchen wird also in Bewegungsenergie des Kolbens umgewandelt, geht den Gasteilchen also verloren, was sich dann durch Temperaturerniedrigung äußert (denn Bewegungsenergie der Teilchen ist ja Temperatur).

Mehr zu Motoren und Kreisprozessen finden Sie hier: Dampfmaschine
& Co.

Der Joule-Thomson-Effekt

Beim Joule-Thomson-Versuch wird ein Gas entspannt, indem es durch ein Drosselventil von einem kleinen Volumen V₁ bei hohem Druck P₁ (links) in ein großes Volumen V₂ bei kleinem Druck P₂ (rechts) strömt. Zwei Kolben (rot) halten rechts und links den Druck konstant. Die Temperatur T₁ ist vorgegeben. Die Anordnung ist thermisch isoliert, der Vorgang verläuft also adiabatisch. Links wird also die Arbeit P₁V₁ am Gas geleistet, rechts die Arbeit –P₂V₂ vom Gas wieder abgegeben.

(Das Gas wird durch ein Drosselventil (blau) gepresst, dessen Aufgabe es ist, die Strömungsgeschwindigkeiten vernachlässigbar klein zu halten, damit der 1. Hauptsatz der Thermodynamik anwendbar ist, ohne dass man Strömungsenergien berücksichtigen muss. Der 1. Hauptsatz ist der, der besagt, dass die Energie eines abgeschlossenen Systems konstant ist beziehungsweise dass ihre Änderung genau der zu- oder abgeführten Arbeit oder Wärme entspricht.)

  Abb. 2 ¦ Joule-Thomson-Versuch  

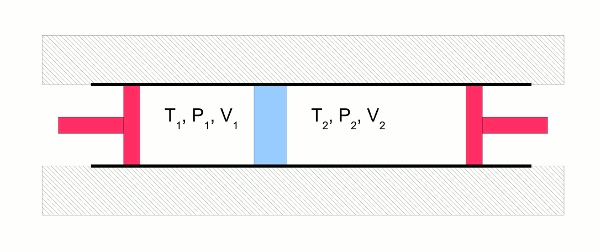
Bei diesem Versuch zeigt sich, dass für ideale Gase die Temperatur des Gases im Anfangs- und im Endzustand dieselbe ist: T₁ = T₂. (Man kann den Versuch natürlich nicht mit idealen Gasen machen – aber je „idealer“ ein Gas ist, desto geringer ist die Temperaturdifferenz zwischen T₁ und T₂.) Die innere Energie U ändert sich damit ebenfalls nicht: U₁ = U₂. Wärmeaustausch mit der Umgebung findet nicht statt (weil der Vorgang ja adiabatisch ist), deshalb muss also auch die Arbeit, die links am Gas geleistet wurde, gleich der sein, die das Gas rechts wieder abgibt: P₁V₁ = P₂V₂.
Das ist der Unterschied zu der adiabatischen Expansion beispielsweise im Zylinder eines Motors oder beim carnotschen Kreisprozess – dort wird vom Gas am Kolben Arbeit verrichtet und es ändert sich die innere Energie des Gases (sie nimmt ab bei einer Expansion) und zwar sowohl für ideale als auch für reale Gase.
Beim Joule-Thomson-Versuch dagegen bleibt die innere Energie für ideale Gase gleich und es wird keine Arbeit verrichtet (bei idealen Gasen!).

Für reale Gase sieht das jedoch anders aus. Bei der adiabatischen Expansion realer Gase ändert sich die Temperatur nämlich und damit auch die innere Energie. Die Differenz U₂ – U₁ muss nach dem 1. Hauptsatz der Differenz der Arbeiten P₁V₁ – P₂V₂ entsprechen:

U₂ − U₁ = P₁V₁ – P₂V₂, oder: U₂ + P₂V₂ = U₁ + P₁V₁.

Die Summe U + PV ergibt eine neue Größe, die Enthalpie H = U + PV. Statt der inneren Energie U bleibt hier also H erhalten, der Vorgang ist isenthalp.

Bei realen Gasen wird also Arbeit verrichtet – es ist P₁V₁ ≠ P₂V₂. Das liegt an den Wechselwirkungen zwischen den realen Gasteilchen – die Teilchen idealer Gase wechselwirken nicht miteinander (außer durch direkte Stöße). In realen Gasen dagegen gibt es zum einen anziehende (Van-der-Waals-)Kräfte zwischen den Molekülen; gegen diese Kräfte muss das reale Gas Arbeit leisten, wenn es expandiert. Diese Arbeit wird der inneren Energie U entnommen und U somit erniedrigt – und damit auch die Temperatur des Gases. Zum anderen haben reale Gasteilchen aber auch eine räumliche Ausdehnung, das heißt, wenn sie sich zu nah kommen, gibt es abstoßende Kräfte. Wenn diese überwiegen, führt eine Expansion dem Gas Arbeit zu und erhöht seine innere Energie und Temperatur. Welche der beiden Kräfte überwiegen, hängt von der Umgebungstemperatur ab – oberhalb der Inversionstemperatur überwiegt die Abstoßung und eine isenthalpe Expansion führt zu einer Temperaturerhöhung, unterhalb der Inversionstemperatur überwiegt die Anziehung und isenthalpe Expansion führt zu einer Temperaturerniedrigung.

Die Verflüssigung eines Gases durch Druckerniedrigung ist daher nur bei Temperaturen unterhalb der Inversionstemperatur möglich – denn hierzu braucht man ja eine durch Expansion hervorgerufene Abkühlung. Bei Helium und Wasserstoff liegt die Inversionstemperatur unterhalb der Raumtemperatur – zunächst liegt die Temperatur der Gase also oberhalb der Inversionstemperatur, weshalb sie erst einmal vorgekühlt werden müssen.